'분류 전체보기'에 해당되는 글 137건

2011.01.22 OpenGL|ES 1.0 2D 튜토리얼 1/2 [출처] OpenGL|ES 1.0 2D 튜토리얼 1/2|작성자 똥라면
2011.01.22 html+css 회전 각도에 따라 각각 다른 css 부여하기
2011.01.11 폴리곤 왜곡 #2
2011.01.11 폴리곤 왜곡 #1
2011.01.08 [Canvas] canvas 11. Image
2011.01.08 [Canvas] canvas 예제. - 복합 도형.
2011.01.08 [Canvas] canvas 10. path도형 그리기 - 사각형.
2011.01.08 [Canvas] canvas 9. path도형 그리기 - 2차곡선,베지어곡선
2011.01.08 [Canvas] canvas 8. path도형 그리기 - 원,호
2011.01.08 [Canvas] canvas 7. path도형 그리기 - 직선

OpenGL|ES 1.0 2D 튜토리얼 1/2 [출처] OpenGL|ES 1.0 2D 튜토리얼 1/2|작성자 똥라면

아이폰에서 OpenGL|ES 1.0을 사용하여 2D를 사용하기위해

먼저 3D의 기본지식을 설명하려 합니다.

http://en.wikipedia.org/wiki/OpenGL_ES <-외국어로 씌어져 있슴.

사용환경

xcode 3.2.5

iOS sdk 4.2

1.우선 OpenGL프로젝트 생성.

저는 GL2D 란 이름으로 생성함.

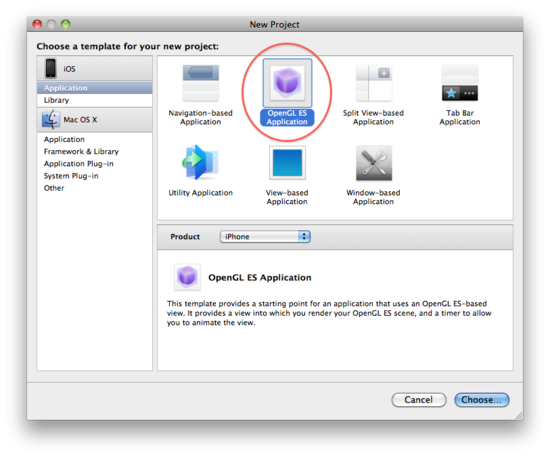
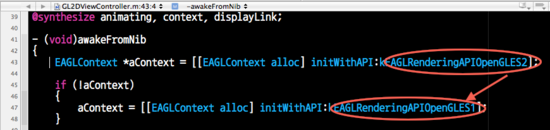
2.OpenGL|ES 1.0을 쓰기위해선 자동생성된 ViewController 43번째줄만 바꿔주면 됩니다.

45~48번줄은 삭제하고 kEAGLRenderingAPIOpenGLES2를 kEAGLRenderingAPIOpenGLES1로 바꿔줌.

//opengl|es 1.0 사용

EAGLContext *aContext = [[EAGLContext alloc] initWithAPI:kEAGLRenderingAPIOpenGLES1];

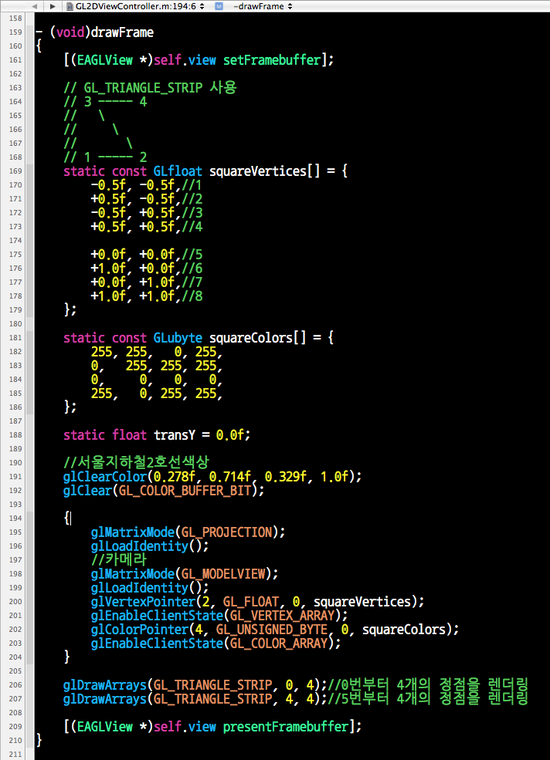
3.이번엔 실질적으로 렌더링하는곳을 몇군데 만져줍니다.

알기쉽게 사각형 순서를 코멘트하고,(163라인)

샘플의 사각형의 세로가 0.333 인게 기분나뻐서 0.5로 변경,(170~174라인)

3D좌표 설명용으로 검정색 정사각형을 하나로 추가하고(175~178라인)

배경색이 어두운게 기운이 안나서 서울지하철2호선색상으로 변경,(191라인)

2.0용 쉐이더 사용하는곳을 지워주고,(193라인근방)

위아래로 움직이는게 멀미할것 같으니 삭제,(200라인근방)

마지막으로 검정색 정사각형을 렌더링합니다.(207라인)-코멘트에 5번부터라고 써있는데 오타임;

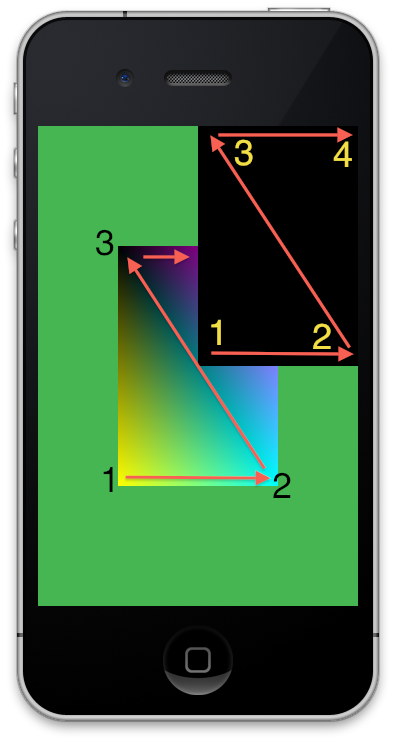
4.빌드하고 실행하면 나오는 결과물입니다.

배경은 서울지하철 2호선 색상이고,

원래 샘플의 사각형보단 약간 길쭉하게 표시되고 정가운데에서 멈춰있으며,

제가 추가한 검정색 정사각형이 보입니다.

거기에 제가 코멘트에 적은 사각형 순서번호를 그렸습니다.

5.제가 추가한 사각형은 가로세로 1.0의 사이즈의 정사각형인데 직사각형으로 나옵니다.

원래 샘플의 사각형도 -0.5~0.5의 사이즈면 결국 1.0의 사이즈인데 마찬가지로 직사각형으로 나옵니다.

허나 이건 틀린게 아닙니다.

세로가 길던 가로가 길던 기본적인 3D좌표는

가운데가 원점

위아래(+1.0 ~ -1.0)

좌우(-1.0 ~ +1.0) 입니다.

( Z축은 왼손좌표일경우 앞뒤 +1.0 ~ -1.0 오른손좌표일경우 앞뒤 -1.0 ~ +1.0 )

제가 추가한 사각형은 사이즈가 1.0이니 위로 길죽하지만

원점을 기준으로 정확하게 1.0의 사이즈로 출력되었고,

원래 샘플의 정사각형도 원점을 기준으로 위아래좌우로 0.5씩의 사이즈로 출력되었습니다.

그러므로 결론은 여기까진 아무문제 없다 입니다.

다음번엔 소스코드에 한줄만 추가해서 정사각형으로 만들고,

알기쉬운 2D좌표를(왼쪽위가 원점)써서 출력을 해볼까 합니다;

[출처] OpenGL|ES 1.0 2D 튜토리얼 1/2|작성자 똥라면

저작자표시 비영리 변경금지

'프로그래밍 > OpenGL-ES' 카테고리의 다른 글

OpenGL\|ES 1.0 2D 텍스쳐 맵핑 1/2 [출처] OpenGL\|ES 1.0 2D 텍스쳐 맵핑 1/2\|작성자 똥라면 (0)	2011.01.22
OpenGL\|ES 1.0 2D 튜토리얼 2/2 [출처] OpenGL\|ES 1.0 2D 튜토리얼 2/2\|작성자 똥라면 (0)	2011.01.22
백버퍼 접근 (0)	2010.08.03
게임 프로젝트 생성할때, (게임은 OpenGl,Ui 는 xib 로...) (0)	2010.07.20

Posted by windship

html+css 회전 각도에 따라 각각 다른 css 부여하기

|

Tip&Tech

0

/

2011.01.19 14:19

하얀고래(audrms8)

준회원

http://cafe.naver.com/mcbugi/103604

말 그대로 회전 각도에 따라 각각 다른 css를 부여하는 방법 입니다.

예를 들어 세로로 볼때 가로로 볼때 각각 다른 스타일이 적용됩니다.

sdk를 능숙하게 다르는 프로그래머라면 필요없겠지만, 저처럼 Objective-C나 sdk를 잘 못다뤄서 HTML+java+CSS로 작업하시는 분들..

또는 아이폰이나 아이패드용 웹사이트 만드시는 분들께 유용한 정보가 되리라 생각 합니다.

몇날 방법을 알아내려고 여기저기 뒤져봤는데 한국에선 워낙 프로그래머 분들 능력이 뛰어나서

html 엡 관련 정보는 잘 찾아볼 수가 없군요.

몇가지 찾아낸 정보는 아무리 적용해도 복잡하게 얽혀있는건지 제가 잘 못한건지 적용이 안되고..

결국 일본어를 좀 알아서 일본어 사이트에서 알아낸 정보 입니다.

별거 아니라고 생각하는 분들도 물론 계시겠지만 저처럼 엄청 유용한 정보가 될지도 모를 분들을 위해 남깁니다.

결론은 정말 정말 간단합니다.

어렵게 자바써서 나눠주고 body에 뭐 써넣고 그런거 일체 없이 아래 딱 두줄만 <head></head>사이에 넣어주면 끝납니다.

해결하고 나서 보니 허무하리만큼 너무 간단하더군요.

잡지 어플 같은거 만드시는분들께 유용하리라 생각합니다.

회전시 화면 확대 뿐만이 아니라 이미지 사이즈조정등 화면 형태에 맞춰 전체적인 스타일이 바뀌면 더 재밌는 엡을 구현할 수 있으리라 생각 되는군요.

추신; html+java+css로 엡 만드는법 잘 나온 사이트나 정보 있으신 분들 공유 부탁 드립니다.

저작자표시 비영리 변경금지

'모바일 WEB 관련' 카테고리의 다른 글

아이폰 웹어플리케이션 개발시 꼭 알아야할것 (0)	2010.06.05
웹페이지 열때 브라우저 종류 인식하기 (0)	2010.06.03
아이폰에서 웹페이지 띄울 때 주소창 자동으로 숨겨주는 처리 (0)	2010.06.03
아이폰용 웹페이지 해상도 최적화 (0)	2010.06.03

Posted by windship

폴리곤 왜곡 #2

Schwarz–Christoffel mapping

From Wikipedia, the free encyclopedia

(Redirected from Schwarz-Christoffel mapping)

In complex analysis, a Schwarz–Christoffel mapping is a conformal transformation of the upper half-plane onto the interior of a simple polygon. Schwarz–Christoffel mappings are used in potential theory and some of its applications, including minimal surfaces and fluid dynamics. They are named after Elwin Bruno Christoffel andHermann Amandus Schwarz.

[edit]Definition

Consider a polygon in the complex plane. The Riemann mapping theorem implies that there is a bijective biholomorphic mapping f from the upper half-plane

$\{ \zeta \in \mathbb{C}: \operatorname{Im}\,\zeta > 0 \}$

to the interior of the polygon. The function f maps the real axis to the edges of the polygon. If the polygon has interior angles $\alpha,\beta,\gamma, \ldots$ , then this mapping is given by

$f(\zeta) = \int^\zeta \frac{K}{(w-a)^{1-(\alpha/\pi)}(w-b)^{1-(\beta/\pi)}(w-c)^{1-(\gamma/\pi)} \cdots} \,\mbox{d}w$

where $K$ is a constant, and $a < b < c < ...$ are the values, along the real axis of the $ζ$ plane, of points corresponding to the vertices of the polygon in the $z$ plane. A transformation of this form is called a Schwarz–Christoffel mapping.

It is often convenient to consider the case in which the point at infinity of the $ζ$ plane maps to one of the vertices of the $z$ plane polygon (conventionally the vertex with angle $α$ ). If this is done, the first factor in the formula is effectively a constant and may be regarded as being absorbed into the constant $K$ .

[edit]Example

Consider a semi-infinite strip in the $z$ plane. This may be regarded as a limiting form of a triangle with vertices $P = 0$ , $Q = π i$ , and $R$ (with $R$ real), as $R$ tends to infinity. Now $α = 0$ and $β = γ = π ⁄ 2$ in the limit. Suppose we are looking for the mapping $f$ with $f (-1) = Q$ , $f (1) = P$ , and $f (\infty) = R$ . Then $f$ is given by

$f(\zeta) = \int^\zeta \frac{K}{(w-1)^{1/2}(w+1)^{1/2}} \,\mbox{d}w. \,$

Evaluation of this integral yields

z > = f (ζ) = C + K ar cosh ζ

where $C$ is a (complex) constant of integration. Requiring that $f (-1) = Q$ and $f (1) = P$ gives $C = 0$ and $K = 1$ . Hence the Schwarz–Christoffel mapping is given by

z = ar cosh ζ

This transformation is sketched below.

Schwarz–Christoffel mapping of the upper half-plane to the semi-infinite strip

[edit]
Other simple mappings

[edit]Triangle

A mapping to a plane triangle with angles $\pi a,\, \pi b$ and $π(1 - a - b)$ is given by

$z=f(\zeta)=\int^\zeta \frac{dw}{(w-1)^{1-a} (w+1)^{1-b}}.$

[edit]Square

The upper half-plane is mapped to the square by

$z=f(\zeta) = \int^\zeta \frac {\mbox{d}w}{\sqrt{w(w^2-1)}} =\sqrt{2} \, F\left(\sqrt{\zeta+1};\sqrt{2}/2\right).$

where F is the incomplete elliptic integral of the first kind.

[edit]General triangle

The upper half-plane is mapped to a triangle with circular arcs for edges by the Schwarz triangle map.

[edit]See also

The Schwarzian derivative appears in the theory of Schwarz–Christoffel mappings.

[edit]References

Driscoll, Tobin A.; Trefethen, Lloyd N. (2002), Schwarz-Christoffel mapping, Cambridge Monographs on Applied and Computational Mathematics, 8, Cambridge University Press, MR 1908657, ISBN 978-0-521-80726-5
Nehari, Zeev (1982) [1952], Conformal mapping, New York: Dover Publications, MR 0045823, ISBN 978-0-486-61137-2

[edit]Further reading

Case, James (2008), "Breakthrough in Conformal Mapping", SIAM News 41 (1).

[edit]External links

저작자표시 비영리 변경금지

'기반지식 > 알고리즘' 카테고리의 다른 글

폴리곤 왜곡 #1 (0)	2011.01.11

Posted by windship

폴리곤 왜곡 #1

Complex Barycentric Coordinates with Applications to Planar Shape Deformation

Ofir Weber Mirela Ben-Chen Craig Gotsman

Eurographics 2009 - Computer Graphics Forum 28, 2 (2009)
Gunter Enderle Best Paper Award

Image deformation using Point-to-Point complex barycentric coordinates.
Click on the image for hi-res version

Abstract:

Barycentric coordinates are heavily used in computer graphics applications to generalize a set of given data values. Traditionally, the coordinates are required to satisfy a number of key properties, the first being that they are real and positive. In this paper we relax this requirement, allowing the barycentric coordinates to be complex numbers. This allows us to generate new families of barycentric coordinates, which have some powerful advantages over traditional ones. Applying complex barycentric coordinates to data which is itself complex-valued allows to manipulate functions from the complex plane to itself, which may be interpreted as planar mappings. These mappings are useful in shape and image deformation applications. We use Cauchy뭩 theorem from complex analysis to construct complex barycentric coordinates on (not necessarily convex) polygons, which are shown to be equivalent to planar Green coordinates. These generate conformal mappings from a given source region to a given target region, such that the image of the source region is close to the target region. We then show how to improve the Green coordinates in two ways. The first provides a much better fit to the polygonal target region, and the second allows to generate deformations based on positional constraints, which provide a more intuitive user interface than the conventional cage-based approach. These define two new types of complex barycentric coordinates, which are shown to be very effective in interactive deformation and animation scenarios.

Paper - PDF:

Supplementary Material - PDF:

Video - QuickTime (H264):

BibTeX entry:

@article{Complex_Coordinates:2009,
author = {Ofir Weber and Mirela Ben-Chen and Craig Gotsman},
title = {Complex Barycentric Coordinates with Applications to Planar Shape Deformation},
journal = {Computer Graphics Forum (Proceedings of Eurographics)},
volume = {28},
number = {2},
year = {2009},
}

More examples:

Comparison of the Point-to-Point Cauchy-Green complex barycentric coordinates and the MLS similarity coordinates.
(left to right) Original image; Deformation using Point-to-Point coordinates; Deformation using MLS coordinates.
The Point-to-Point coordinates better handle control points whose Euclidean distance is small, yet their geodesic distance within the cage is large.
Click on the image for hi-res version

Deformation of a bird using Szego coordinates. The cage has 21 vertices.
Click on the image for hi-res version

A giraffe (left), and its deformation (right) using Point-to-point Cauchy-Green coordinates, with 16 control points. The cage has 113 vertices.
Click on the image for hi-res version

Color-coded visualization of one P2P coordinate function. (left to right) Real part; Imaginary part; Absolute value.
Click on the image for hi-res version

저작자표시 비영리 변경금지

'기반지식 > 알고리즘' 카테고리의 다른 글

폴리곤 왜곡 #2 (0)	2011.01.11

Posted by windship

[Canvas] canvas 11. Image

캔바스의 더 재밌는 기능중에 하나는 바로 이미지를 바로 가져다 쓴다는점입니다. 거의 모든 이미지들을 지원하는 덕분에 이미지의 큰 제약없이 사용할수가 있습니다.

이미지를 불러오기위해서는 두가지절차가 필요합니다.
1. 이미지 객체를 생성하기.
2. 생성된 이미지 객체에 이미지를 넣기.

이미지를 가져오는 방법에는 기본적으로 네가지정도를 쓰고 있는데요.

같은 페이지에있는 이미지를 가져올때.
-document.images 메소드나 document.getElementsByTagName , document.getElementById 메소드 들을 이용하여 가져오는 방법.

다른 캔바스 요소를 가져올때
- 마찬가지로 document.getElementsByTagName , document.getElementById 메소드를 사용하여 다른 캔바스의 이미지를 가져올수 있습니다. 가져오기전에 캔바스에 어떤그림을 그려놓았는지 확인은 필수 :)

처음부터 만들기
- 스크립트를 이용하여 직접 이미지를 만드는방법이 되겠습니다. 이방법은 스크립트가 실행되는 시점에 이미지 파일이 로딩되기때문에 필요에따라서는 프리로딩이 필요할수도 있습니다.

이미지 객체를 기본 생성하려면 다음과 같이 하면 됩니다.

var img = new Image(); // Create new Image object

img.src = 'myImage.png'; // Set source path

이렇게 될경우 이 스크립트가 실행되는 시점에서 이미지가 로딩이 일어나고, 이미지가 로딩이 완료되기 전에는 다음 스크립트가 실행되지 않습니다. 이점 참고하시기 바랍니다.
그래서 onload 이벤트 등에 미리 이미지를 프리로딩하는 방법을 쓰기도 합니다.

data: url 방식의 이미지 추가하기

또 다른 이미지 불러오는 방법으로 data:url 방식이 있습니다. 이놈은 링크자체에 base64 로 완전히 인코딩된 url 링크를 직접 사용할수 있습니다. 이 방법은 링크를 숨겨주는등의 몇가지 장점이 있으나 캐쉬되지않아 큰 이미지의경우 오히려 사이트 속도에 큰 영향을 줄수도 있습니다.

var img_src = 'https://t1.daumcdn.net/cfile/tistory/2660F84256E67F581A"font-family: Tahoma, 굴림; font-size: 9pt; color: rgb(34, 34, 34); margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; padding-top: 0px; padding-right: 0px; padding-bottom: 0px; padding-left: 0px; ">위와같이 사용하게 됩니다.

이미지 그리기

그럼 실제로 이미지를 캔바스에 그려보도록 하겠습니다.

이미지를 캔바스에 그리는데는

drawImage(image, x, y)

이 함수가 필요합니다. 이미지 객체와 x,y 좌표가 필요하지요.
캔바스에 이미지를 그려준 뒤에는 그 이미지 위에 라인이나 path도형등을 그려줄수 있습니다.
예제를 보며 설명하도록 하겠습니다.

[출처]모질라 캔바스 튜토리얼

미리보기

function draw() {  

    var ctx = document.getElementById('canvas').getContext('2d');  

    var img = new Image();  

    img.onload = function(){  

      ctx.drawImage(img,0,0);  

      ctx.beginPath();  

      ctx.moveTo(30,96);  

      ctx.lineTo(70,66);  

      ctx.lineTo(103,76);  

      ctx.lineTo(170,15);  

      ctx.stroke();  

}

    img.src = 'images/backdrop.png';  

}

위의 함수는 기본적인 그래프를 그려주는 함수 인데요. X와 Y축라인을 이미지를 불러와 그려준뒤

path도형으로 그래프 라인을 그려주고 마무리한 예제 입니다.

저작자표시 비영리 변경금지

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

[Canvas] canvas 예제. - 복합 도형. (0)	2011.01.08
[Canvas] canvas 10. path도형 그리기 - 사각형. (0)	2011.01.08
[Canvas] canvas 9. path도형 그리기 - 2차곡선,베지어곡선 (0)	2011.01.08
[Canvas] canvas 8. path도형 그리기 - 원,호 (0)	2011.01.08
[Canvas] canvas 7. path도형 그리기 - 직선 (0)	2011.01.08

Posted by windship

[Canvas] canvas 예제. - 복합 도형.

복합도형 예제.

그동안 설명했던 내용을 대부분 포함하여 그림을 그려보았습니다.

각 path 부분을 함수화 시키고 사용한다면 간단한 모션까지는 가능할수도 있겠지요?

참고하시기 바랍니다

미리보기

function draw() {

var ctx = document.getElementById('canvas').getContext('2d');

roundedRect(ctx,12,12,150,150,15);

roundedRect(ctx,19,19,150,150,9);

roundedRect(ctx,53,53,49,33,10);

roundedRect(ctx,53,119,49,16,6);

roundedRect(ctx,135,53,49,33,10);

roundedRect(ctx,135,119,25,49,10);

ctx.beginPath();

ctx.arc(37,37,13,Math.PI/7,-Math.PI/7,true);

ctx.lineTo(31,37);

ctx.fill();

for(var i=0;i<8;i++){

ctx.fillRect(51+i*16,35,4,4);

}

for(i=0;i<6;i++){

ctx.fillRect(115,51+i*16,4,4);

}

for(i=0;i<8;i++){

ctx.fillRect(51+i*16,99,4,4);

}

ctx.beginPath();

ctx.moveTo(83,116);

ctx.lineTo(83,102);

ctx.bezierCurveTo(83,94,89,88,97,88);

ctx.bezierCurveTo(105,88,111,94,111,102);

ctx.lineTo(111,116);

ctx.lineTo(106.333,111.333);

ctx.lineTo(101.666,116);

ctx.lineTo(97,111.333);

ctx.lineTo(92.333,116);

ctx.lineTo(87.666,111.333);

ctx.lineTo(83,116);

ctx.fill();

ctx.fillStyle = "white";

ctx.beginPath();

ctx.moveTo(91,96);

ctx.bezierCurveTo(88,96,87,99,87,101);

ctx.bezierCurveTo(87,103,88,106,91,106);

ctx.bezierCurveTo(94,106,95,103,95,101);

ctx.bezierCurveTo(95,99,94,96,91,96);

ctx.moveTo(103,96);

ctx.bezierCurveTo(100,96,99,99,99,101);

ctx.bezierCurveTo(99,103,100,106,103,106);

ctx.bezierCurveTo(106,106,107,103,107,101);

ctx.bezierCurveTo(107,99,106,96,103,96);

ctx.fill();

ctx.fillStyle = "black";

ctx.beginPath();

ctx.arc(101,102,2,0,Math.PI*2,true);

ctx.fill();

저작자표시 비영리 변경금지

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

[Canvas] canvas 11. Image (0)	2011.01.08
[Canvas] canvas 10. path도형 그리기 - 사각형. (0)	2011.01.08
[Canvas] canvas 9. path도형 그리기 - 2차곡선,베지어곡선 (0)	2011.01.08
[Canvas] canvas 8. path도형 그리기 - 원,호 (0)	2011.01.08
[Canvas] canvas 7. path도형 그리기 - 직선 (0)	2011.01.08

Posted by windship

[Canvas] canvas 10. path도형 그리기 - 사각형.

할까말까 고민했습니다만..

다 하나씩 했으니 그래도 강좌 하나 잡아먹고 들어가겠습니다.

rect(x, y, width, height)

사각형입니다. 좌표와 가로세로 크기를 지정해주면 그려줍니다.

예제도 이미지도 넣지 않겠습니다 참고만 하시길 :)

저작자표시 비영리 변경금지

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

[Canvas] canvas 11. Image (0)	2011.01.08
[Canvas] canvas 예제. - 복합 도형. (0)	2011.01.08
[Canvas] canvas 9. path도형 그리기 - 2차곡선,베지어곡선 (0)	2011.01.08
[Canvas] canvas 8. path도형 그리기 - 원,호 (0)	2011.01.08
[Canvas] canvas 7. path도형 그리기 - 직선 (0)	2011.01.08

Posted by windship

[Canvas] canvas 9. path도형 그리기 - 2차곡선,베지어곡선

다음 속성으로는 베지어 곡선에 대해서 알아보겠습니다.

입방체 혹은 정사각형에 사용할수있는 곡선인데요. 이게 말로는 참 설명하기 거시기 한것이긴하지만

여차저차 설명은 해보겠습니다.

quadraticCurveTo(cp1x, cp1y, x, y) // 파폭 1.5에서 동작하지 않는듯.

bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)

곡선을 나타내는 두개의 함수가 있는데요 둘다 용도가 비슷한듯하지만 많이 다릅니다.

일단 이미지를 한번 보시겠습니다.

[사진출처]모질라 캔바스 튜토리얼

quadraticCurveTo 함수는 이미지에서 보듯이 곡선의 기준점이 하나입니다.

cp1x,cp1y 두개의 기준점과 x,y 라인의 끝점.

두개의 좌표값으로 곡선을 그리게 됩니다.

학교시절 배운 2차원 곡선에대해서 떠올리면 쉬울것같은데요.

여기에서 기준점이 하나 더 추가된것이 베지어 곡선입니다.

베지어곡선은 무슨 베지어란양반이 포드자동차를 CAD로 디자인하면서 썼는데 그게 유명해져서

그의 이름이 붙었다고합니다.

베지어가 고안한것은아니고 사실 그 개념은 그이전부터 존재했다고 하니 창시자는 아니겠네요.

사설이 길어졌는데. 베지어 곡선은 그림으로는 설명이 부족하니 위키피디아 이미지를 잠깐 인용해보겠습니다.

[사진출처] 위키피디아.

위와같은 곡선이 그려지게 됩니다. 이제 베지에곡선의 포인트가 두개인 이유를 아시겠지요?

P1, P2 가 곡선의 포인트 좌표가되고 P3이 곡선이 끝나는좌표, x,y 가 되는겁니다.

물론 베지에 곡선은 기준점이 2개가 아니라 n개 즉 여러개가 될수있고 2차원 그래프가아닌3차 4차원 그래프도

그려질수 있으며

일부 폰트에서 글자를 부드럽게 하는데도 사용된다고 합니다.... 만

지원하는 함수에서는 2포인트만 지원하는군요. 뭐 이정도면 충분하고 응용법도 있으니 괜찮습니다.

그럼 먼저 quadraticCurveTo 를 이용해서 말풍선을 하나 그려보겠습니다.

// Quadratric curves example

ctx.beginPath();

ctx.moveTo(75,25);

ctx.quadraticCurveTo(25,25,25,62.5);

ctx.quadraticCurveTo(25,100,50,100);

ctx.quadraticCurveTo(50,120,30,125);

ctx.quadraticCurveTo(60,120,65,100);

ctx.quadraticCurveTo(125,100,125,62.5);

ctx.quadraticCurveTo(125,25,75,25);

ctx.stroke();

[사진출처]모질라 캔바스 튜토리얼

따로 예제는 제공하지 않겠습니다.

그리고 이번에는 베지에함수를 이용한 하트.

// Bezier curves example

ctx.beginPath();

ctx.moveTo(75,40);

ctx.bezierCurveTo(75,37,70,25,50,25);

ctx.bezierCurveTo(20,25,20,62.5,20,62.5);

ctx.bezierCurveTo(20,80,40,102,75,120);

ctx.bezierCurveTo(110,102,130,80,130,62.5);

ctx.bezierCurveTo(130,62.5,130,25,100,25);

ctx.bezierCurveTo(85,25,75,37,75,40);

ctx.fill();

[사진출처]모질라 캔바스 튜토리얼

역시 예제는 따로 제공하지 않습니다.

p.s : 파폭 1.5 에서는 quadraticCurveTo 함수에 뭔가 치명적인 버그가 있다고 합니다만

1.5 버젼까지 설치해서 테스트 해볼 생각이 없습니다. 알고만 계시면 될것같네요.

저작자표시 비영리 변경금지

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

[Canvas] canvas 예제. - 복합 도형. (0)	2011.01.08
[Canvas] canvas 10. path도형 그리기 - 사각형. (0)	2011.01.08
[Canvas] canvas 8. path도형 그리기 - 원,호 (0)	2011.01.08
[Canvas] canvas 7. path도형 그리기 - 직선 (0)	2011.01.08
[Canvas] canvas 6. path도형 그리기 (0)	2011.01.08

Posted by windship

[Canvas] canvas 8. path도형 그리기 - 원,호

원이나 호를 그리기 위해서는 arc 메소드가 사용됩니다. 사파리와 파이어폭스에서 지원하는

arcTo 메소드 역시 설명에 포함되지만, 이전 버젼에서는 지원하질 않습니다.

arc(x, y, radius, startAngle, endAngle, anticlockwise)

이 메소드는 다섯가지 파라메터를 가지고 있는데 x와 y는 원의 중심좌표를 나타내고

radius 는 말그대로 반지름이고 startAngle과 endAngle은 호의 시작과 끝을 나타내는

포인트입니다.

호의 시작과 끝을 나타내는 각도는 x축을 기준으로 계산되어 지고있습니다. (x축이 0도라는말)

anticlockwise 은 방향을 나타내는데요 true 일경우 시계방향으로 false일경우

반대방향입니다.

NOTE:

여기에서 라디안을 설명하지 않고 넘어갈수가 없는데요. 보통 수학시간에 배우는 rad로

를 떠올리시면 될듯한데요. 호도법이라고도 합니다. arc 메소드는 각도가 아니라

라디안으로 호의 크기를 계산합니다.

라디안은 원의 반지름과 같은 길이를 갖는 호(弧)가 이루는 각을 말합니다.

원주는 2π×반지름과 같습니다 그러므로 1라디안=360/(2π)＝180/π＝약 57.2958이되는거죠

반대로 도수×π/180＝라디안 수가 됩니다. 즉 360도＝2π라디안 입니다.

그럼 예제를 보면서 이해해 보도록 하겠습니다.

for(var i=0;i<4;i++){

  for(var j=0;j<3;j++){

    ctx.beginPath();

    var x              = 25+j*50;               // x coordinate

    var y              = 25+i*50;               // y coordinate

    var radius         = 20;                    // Arc radius

    var startAngle     = 0;                     // Starting point on circle

    var endAngle       = Math.PI+(Math.PI*j)/2; // End point on circle

    var anticlockwise  = i%2==0 ? false : true; // clockwise or anticlockwise



    ctx.arc(x,y,radius,startAngle,endAngle, anticlockwise);



    if (i>1){

      ctx.fill();

    } else {

      ctx.stroke();

    }

  }

}

예제 보기

예제를 보시면 12개의 서로다른모양의 도형들이 있습니다. 크게 속이 꽉찬 도형과 속이 빈 도형으로

나눌수 있는데요. 이것은 코드 마지막쯤에서 분기해준 fill메소드로 그려주냐 stroke 메소드로

그려주느냐에따라 결정되는 부분이고 쉽게 이해되리라 생각됩니다.

각각의 fill과 strike메소드로 그려진 호들은 역시 위아래로 각각 두줄씩인데요.

anticlockwise 변수의 종류에 따라 달라지는 모습을 보기 위해서 입니다.

그려주는 방향이 다르기때문에 라디안이 같더라도 모양은 반대로 그려지게 되지요.

그리고 각각의 도형들은 루프문에따라 파이를 곱해서 라디안을 결정하도록 했습니다.

라디안의 사용법에대해서는 고등수학에서 나왔던가? 했던거같으니 잘 모르는 분은 공부하시면 되겠습니다

그리 어렵지 않습니다.

저작자표시 비영리 변경금지

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

[Canvas] canvas 10. path도형 그리기 - 사각형. (0)	2011.01.08
[Canvas] canvas 9. path도형 그리기 - 2차곡선,베지어곡선 (0)	2011.01.08
[Canvas] canvas 7. path도형 그리기 - 직선 (0)	2011.01.08
[Canvas] canvas 6. path도형 그리기 (0)	2011.01.08
[Canvas] canvas 5. 도형 그리기 (0)	2011.01.08

Posted by windship

[Canvas] canvas 7. path도형 그리기 - 직선

직선
직선을 그리기 위해서는 lineTo 메소드를 사용합니다.

lineTo(x, y)

이 메소드는 x,y 두가지 인자를 포함하는데. 이 좌표는 직선의 끝점을 나타냅니다.

현재 위치로부터 x,y 좌표까지의 직선을 그려주는 겁니다.

시작점을 바꾸기 위해서는 앞서 살펴보았던 moveTo 메소드를 이용하면 됩니다.

// Filled triangle

ctx.beginPath();

ctx.moveTo(25,25);

ctx.lineTo(105,25);

ctx.lineTo(25,105);

ctx.fill();



// Stroked triangle

ctx.beginPath();

ctx.moveTo(125,125);

ctx.lineTo(125,45);

ctx.lineTo(45,125);

ctx.closePath();

ctx.stroke();

위의 코드를 살펴보면 두개의 삼각형을 그리는 path도형인데요.

첫번째는 내부가 꽉찬 삼각형, 두번째는 내부가 비어있는 삼각형을 그리도록 되어있습니다.

주의할점은 라인을 2개만 사용하여 삼각형을 그렸다는건데요 앞서 살펴보았던 fill 메소드의 특성상

closePath메소드를 사용하지 않아도 자동적으로 도형을 완성시켜줍니다.

시작점과 마지막까지 그린점을 직선으로 이어주어 두개의 선으로 완전한 하나의 도형을 완성시켜주는셈입니다

[사진출처]모질라 캔바스 튜토리얼

물론 라인을 두개만 사용하지않고 끝까지 그려서 완성시켜주셔도 무방합니다.

저작자표시 비영리 변경금지

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

[Canvas] canvas 9. path도형 그리기 - 2차곡선,베지어곡선 (0)	2011.01.08
[Canvas] canvas 8. path도형 그리기 - 원,호 (0)	2011.01.08
[Canvas] canvas 6. path도형 그리기 (0)	2011.01.08
[Canvas] canvas 5. 도형 그리기 (0)	2011.01.08
[Canvas] canvas 4. 간단한예제 (0)	2011.01.08

Posted by windship

'분류 전체보기'에 해당되는 글 137건

'프로그래밍 > OpenGL-ES' 카테고리의 다른 글

'모바일 WEB 관련' 카테고리의 다른 글

Schwarz–Christoffel mapping

Contents

[edit]Definition

[edit]Example

[edit] Other simple mappings

[edit]Triangle

[edit]Square

[edit]General triangle

[edit]See also

[edit]References

[edit]Further reading

[edit]External links

'기반지식 > 알고리즘' 카테고리의 다른 글

'기반지식 > 알고리즘' 카테고리의 다른 글

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

'모바일 WEB 관련 > HTML5' 카테고리의 다른 글

카테고리

공지사항

태그목록

최근에 올라온 글

최근에 달린 댓글

최근에 받은 트랙백

글 보관함

달력

링크

티스토리툴바

[edit]
Other simple mappings